基礎から学ぶ受験数学　＜関数編＞ ~二次関数~

2024年2月18日2024年2月23日

当ページのリンクには広告が含まれています。

今回は二次関数を扱っていきたいと思います。

二次関数は高校数学の最初の関門と言える分野で苦手な人も少なくないと思います。

しかし、二次関数が出来ないと、高校数学は終了します。

なので、二次関数は定型問題がスラスラ解けるぐらいよく学んでください。

うさぎさん

二次関数は慣れれば簡単だよ

今回の内容

二次関数

中学でも $y=x^2$ のように原点を必ず通る二次関数は扱ったと思います。

しかし、高校になると原点を通らない二次関数がほとんどです。

例を出すと $y=x^2+2$, $y=(x-3)^2$ などがあります。

文字を用いて一般化すると

中学の二次関数

高校の二次関数

$y=ax^2$ と表される。

$f(x)=ax^2+bx+c$

$f(x)=a(x-p)^2+q$ と表される。

補足

高校からは $y=$ と書かずに $f(x)=$ と表記します。これは、$x$ に何か文字を代入するとき、楽に書くことが出来るからです。

例えば、$f(x)=x^2$ とすると、$f(0)=0, f(2)=4$ となります。

必要があれば以下の例題を解いてみてください。

例題

$f(x, y, z)=2x^2+3y^2+z^2$ とするとき、下記の問いに答えよ。

（１）$f(x, 1, z)$

（２）$f(x, y, 2)$

（３）$f(1, 1, z)$

解答

（１）\begin{align} f(x, 1, z)&=2x^2+3\cdot1^2+z^2 \\ &=2x^2+z^2+3 \end{align}

（２）\begin{align} f(x, y, 2)&=2x^2+3y^2+2^2 \\ &=2x^2+3y^2+4 \end{align}

（３）\begin{align} f(1, 1, z)&=2\cdot1^2+3\cdot1^2+z^2 \\ &=z^2+5 \end{align}

ここで、重要なのは二次関数の表記法が二つ存在していることです。

一つ例題をいれます、解いてみてください。

例題

$f(x)=ax^2+bx+c$ , $g(x)=a(x-p)^2+q$ $(a\neq0)$ とする時、$p, q$ を $a, b, c$ を用いて表せ。

解答

$g(x)$ の右辺を展開すると

$$g(x)=ax^2-2ap+ap^2+q$$

となるから、係数比較して

\begin{cases} -2ap=b \\ ap^2+q=c \end{cases}

ここで、$a\neq0$ より

$$p=-\frac{b}{2a}$$

$$q=\frac{4ac-b^2}{4a}$$

この問いのように二次関数 $f(x)=ax^2+bx+c$ を $g(x)=a(x-p)^2+q$ の形に変換する操作を平方完成と言います。

平方完成

二次式を $a(x-p)^2+q$ の形に式変形することを平方完成という。

二次関数を見たら平方完成する

二次関数の問題が出た場合は、$f(x)=ax^2+bx+c$ と $g(x)=a(x-p)^2+q$ の両方の形で式を表す作業を最初にするようにしましょう。

理由として、それぞれの形にメリットがあるからです。

$f(x)=ax^2+bx+c$ のメリット

$g(x)=a(x-p)^2+q$ のメリット

$y$切片が分かりやすい
$x$切片が分かりやすい

頂点座標が分かりやすい
グラフが解を持つかが分かりやすい

順に解説していきます。

まず、$f(x)=ax^2+bx+c$ のメリットについて、$y$切片というのは$x=0$の値を入れた際の$y$座標を意味します。

$f(0)=c$ なので $f(x)=ax^2+bx+c$ の形であれば一目で分かります。

また、$x$切片とは $f(x)=0$ を意味するので $ax^2+bx+c=0$ を解けば良いことになります。

つまり、二次方程式を解けば良いことになるので、解の方程式や因数分解を用いることで簡単に解けると思います。

次に、$a(x-p)^2+q$ のメリットについてですが、これはグラフを用いた方が分かりやすいと思います。

二次関数を $a(x-p)^2+q$ と表した場合の頂点は $(p, q)$ になります。よって、頂点座標が分かりやすいです。

また、グラフが解を持つ条件は、二次関数が $x$ 軸との交点を持つかによりますが、これは、$q \le 0$ のとき、解を持つとグラフから明らかです。

このように、それぞれメリットがあるので両方の形で表すようにしましょう。

例題を以下に示すので解いてみてください。

例題

二次関数 $f(x)=ax^2+bx+c$ を平方完成することを考える。以下の問いに答えよ。

（１）$f(x)=a(x^2+dx+e)$ と表すとき、$d, e$ を $a, b, c$ を用いて表せ。

（２）$f(x)=a((x+f)^2+g)$ と表すとき、$f, g$ を $a, b, c$ を用いて表せ。

（３）$a=2, b=3, c=1$ とするとき、$f(x)$ を平方完成せよ。ただし、途中過程を記すこと。

解答

（１）二次関数 $f(x)=ax^2+bx+c$ であるから $a\neq0$ より $a$ で括ると

$$f(x)=a\left(x^2+\frac{b}{a}x+\frac{c}{a}\right)$$

　　　よって、

$$d=\frac{b}{a}$$

$$e=\frac{c}{a}$$

（２）$(x+f)^2+g=x^2+2fx+f^2+g$ であるから $f=\displaystyle\frac{d}{2}, g=e-\displaystyle\frac{d^2}{4}$

　　　よって、

$$f=\frac{b}{2a}$$

$$g=\frac{c}{a}-\frac{b^2}{4a^2}$$

（３）$f(x)=2x^2+3x+1$ を平方完成することを考える。

　　　2を括りだすと $f(x)=2\left(x^2+\displaystyle\frac{3}{2}x+\displaystyle\frac{1}{2}\right)$ となる。

　　　ここで、$x^2+\displaystyle\frac{3}{2}x=\left(x+\displaystyle\frac{3}{4}\right)^2-\left(\displaystyle\frac{3}{2}\right)^2$ であるから

　　　$f(x)=2\left(\left(x+\displaystyle\frac{3}{4}\right)^2-\left(\displaystyle\frac{3}{2}\right)^2+\displaystyle\frac{1}{2}\right)$ となる。

　　　よって、$f(x)=2\left(x+\displaystyle\frac{3}{4}\right)^2-\displaystyle\frac{7}{2}$

これが、平方完成の基本手順となります。平方完成は何回もやって慣れることが重要なので、色々な問題に触れて慣れていきましょう。

例題

以下に示す二次関数が $ax^2+bx+c$ で表されてる場合は $a(x-p)^2+q$ の形に変形し、$a(x-p)^2+q$ の形で表されてる場合は $ax^2+bx+c$ の形に変形せよ。また、頂点、y軸との交点、x軸との交点座標をそれぞれ求めよ。

（１）$f(x)=x^2+2x-3$

（２）$f(x)=x^2-4x+4$

（３）$f(x)=3x^2+6$

（４）$f(x)=(x+2)^2-9$

解答

（１）$f(x)=(x+1)^2-1-3$

　　　$f(x)=(x+1)^2-4$ となるから、頂点座標は $(-1, -4)$

　　　また、$f(x)=0$ のとき、$(x+3)(x-1)=0$ より、x軸との交点座標は $(-3, 0), (1, 0)$

　　　$f(0)=-3$ より、y軸との交点座標は $(0, -3)$

（２）$f(x)=(x-2)^2$ となるから、頂点座標、x軸との交点座標は $(2, 0)$

　　　また、$f(0)=4$ より、y軸との交点座標は $(0, 4)$

（３）頂点座標、x軸との交点座標は $(0, 6)$

　　　また、$f(0)=-9$ より、y軸との交点座標は $(0, -9)$

（４）$f(x)=x^2+4x-5$

　　　$f(x)=(x+2)^2-9$ であるから、頂点座標は $(-2, -9)$

　　　また、$f(x)=0$ のとき、$(x+5)(x-1)=0$ より、x軸との交点座標は $(-5, 0), (1, 0)$

　　　$f(0)=-5$ より、y軸との交点座標は $(0, -5)$

補足

（４）において、x軸との交点座標を求める方法は因数分解をするほかに

$$(x+2)^2-9=0$$

とすることで

$$(x+2)^2=9$$

$$x+2=\pm3$$

よって、$x=-5, x=1$ と求めることもできる。状況によって使い分けてみよう。

二次関数のグラフ

ここからはグラフについて考えていきます。

上図は $y=a(x-p)^2+q$ のグラフで $a, p, q$ を自由に動かせるようにしてあります。

ここで、何個か用語を出しますが覚えるほどのことでもありません。何回か見てるうちに自然に覚えます。

二次関数のグラフ

$(p, q)$ をグラフの頂点という
直線 $x=p$ をグラフの軸という
$a\gt0$ のとき、下に凸という
$a\lt0$ のとき、上に凸という

今すぐに覚える必要はないよ

それでは、具体的なグラフの書き方を紹介します。

STEP

頂点、y切片、x切片の座標を調べる

これらの座標は問題を解く上で必要になることがあるので最初に調べておきましょう。

平方完成をすることで簡単に調べることが出来ると思います。

STEP

$a$ の符号から上に凸か下に凸かを考えてグラフを図示する

基本的に曲線を意識して、頂点、y切片、x切片を通るようにグラフを図示すれば良いです。

グラフを図示する際には、$x$軸、$y$軸、原点、関数式を必ず書くようにしてください。

補足

二次関数の頂点は微分すると傾きが０になっています。つまり、頂点を尖らせたグラフは正確には間違っています。頂点付近はx軸に平行な直線を意識して図示するようにしましょう。

例題

以下の関数の頂点、y切片、x切片を調べ、グラフを図示せよ。

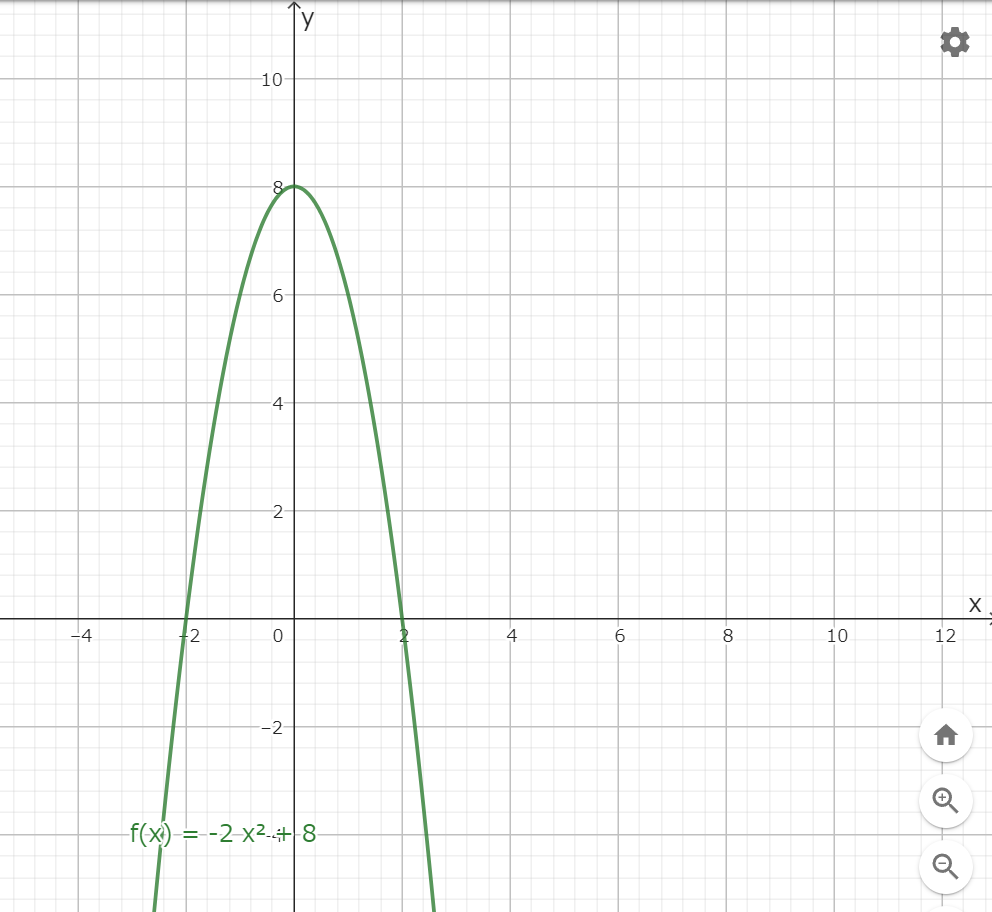
（１）$f(x)=-2x^2+8$

（２）$g(x)=x^2+5x+6$

（３）$h(x)=2x^2-x-1$

解答

（１）$f(0)=8$ より、頂点、$y$切片の座標は $(0, 8)$

　　　$f(x)=0$ とすると、$x=\pm2$ より $y$切片の座標は $(-2, 0), (2, 0)$

　　　よって、求めるグラフは以下のようになる

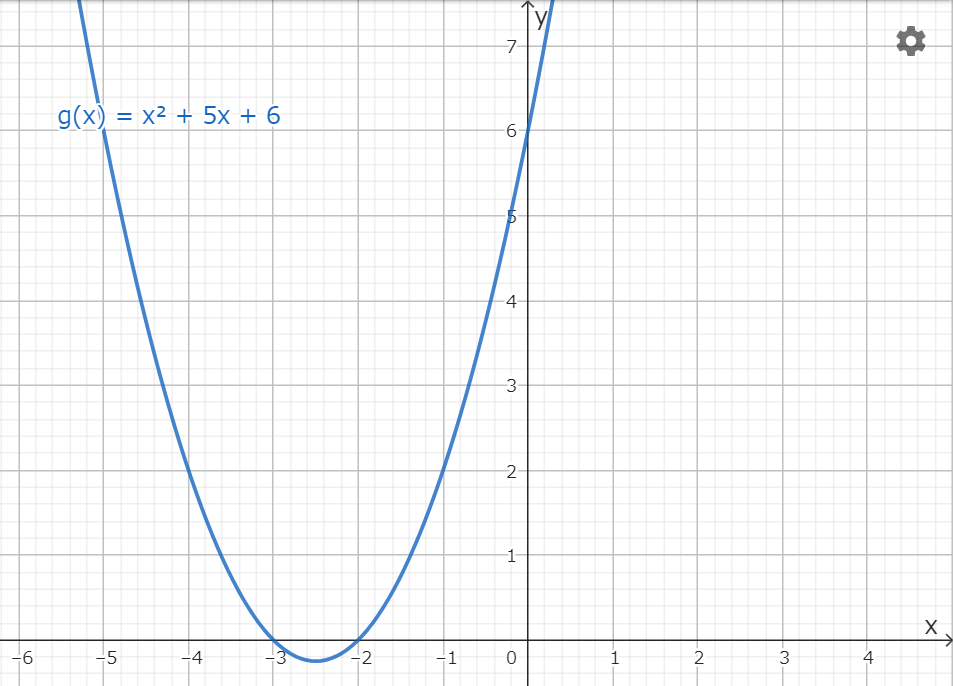
（２）$g(x)=\left(x+\displaystyle\frac{5}{2}\right)^2-\left(\displaystyle\frac{5}{2}\right)^2+\displaystyle\frac{24}{4}$

　　　$g(x)=\left(x+\displaystyle\frac{5}{2}\right)^2-\displaystyle\frac{1}{4}$

　　　$g(0)=6$ より、$y$切片の座標は $(0, 6)$

　　　また、頂点の座標は $\left(-\displaystyle\frac{5}{2}, -\displaystyle\frac{1}{4}\right)$

　　　$g(x)=0$ とすると、$(x+3)(x+2)=0$ より $x$切片の座標は $(-3, 0), (-2, 0)$

　　　よって、求めるグラフは以下のようになる

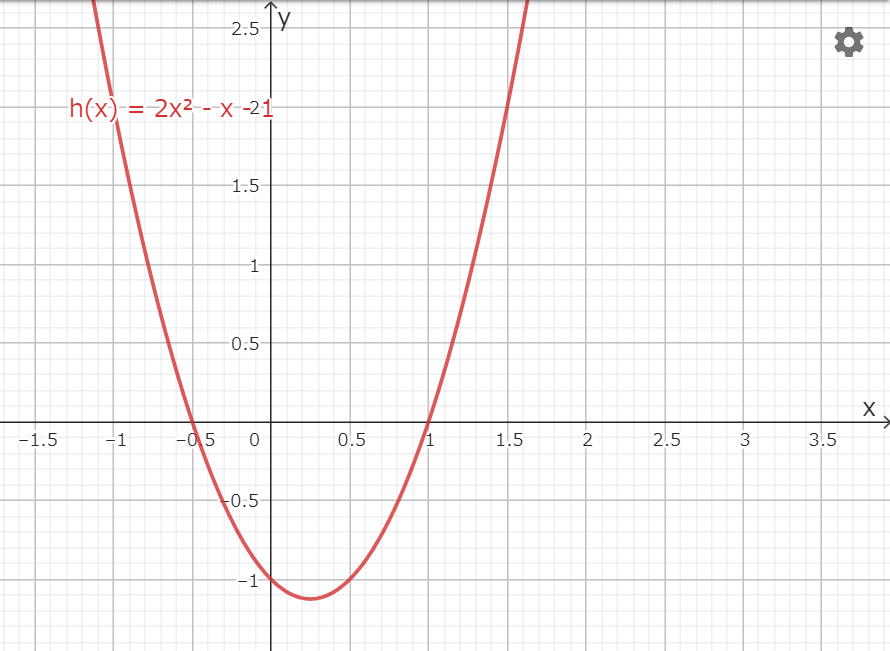
（３）$h(x)=2\left(x^2-\displaystyle\frac{1}{2}x-\displaystyle\frac{1}{2}\right)$

　　　$h(x)=2\left(\left(x-\displaystyle\frac{1}{4}\right)^2-\left(\displaystyle\frac{1}{4}\right)^2-\displaystyle\frac{8}{16}\right)$

　　　$h(x)=2\left(\left(x-\displaystyle\frac{1}{4}\right)^2-\displaystyle\frac{9}{16}\right)$

　　　$h(x)=2\left(x-\displaystyle\frac{1}{4}\right)^2-\displaystyle\frac{9}{8}$

　　　$h(0)=-1$ より、$y$切片の座標は $(0, -1)$

　　　また、頂点の座標は $\left(\displaystyle\frac{1}{4}, -\displaystyle\frac{9}{8}\right)$

　　　$h(x)=0$ とすると、$(2x+1)(x-1)=0$ より $x$切片の座標は $\left(-\displaystyle\frac{1}{2}, 0\right), (1, 0)$

　　　よって、求めるグラフは以下のようになる

うさぎさん

グラフ図示した方が視覚的に分かりやすくなって解ける問題もあるから、関数の問題で図示出来そうなら図示した方が良いよ

二次関数の最大値・最小値

次に、二次関数の最大値と最小値について説明します。

再びグラフを用いて説明します。

もし、$x$の範囲が定められてないのであれば、$a\gt0$ のとき、最小値 $q$、最大値なし

$a\lt0$ のとき、最大値 $q$、最小値なしとなります。

これはグラフから明らかだと思います。

しかし、基本的に最大値・最小値を問う問題では $x$ の範囲が決められています。例を見てみましょう。

例

関数 $f(x)$ を下記のように定める。

$$f(x)=(x-1)^2+1　(a \le x \lt a+3)$$

このとき、$f(x)$ の最大値・最小値を求めよ。

最大値・最小値の問題はグラフを用いて視覚的に解いた方が分かりやすいのでグラフを図示して見ます。

$a$ の値を変えて範囲が移動することを確認してみてください。$x$ の範囲は青い領域に相当します。

ここで、重要なのは点線部分、つまり、不等号において等号が成立しない部分です。

この部分は最大値にも最小値にもなりえません。

今回の場合ですと、$a \gt -\displaystyle\frac{1}{2}$ に右側が範囲における最大値になりますが、等号が成立しないので最大値はなしになります。

このように、範囲に $\lt$ や $\gt$ が含まれる場合は注意してください。

それでは、最大値・最小値の問題に対しての解法を確認していきましょう

STEP

グラフを図示する。

平方完成を用いてグラフを図示します。最大値・最小値の問題で必要になる情報は頂点座標だけなので、$x$ 切片や $y$ 切片は無理に導出しなくても良いです。

STEP

最大値・最小値の変化する座標を調べる。

最大値・最小値問題のポイントはここです。最大値・最小値の問いではほぼ確実に場合分けが必要になります。

今回のように、下に凸のグラフの場合は頂点が範囲に含まれる場合、確実に最小値になります。

なので、最初は最小値について考えていきます。

上図において、$a$ を小さい値から少しずつ動かしてみてください。$a=-2$ のとき、右側が頂点に重なると思います。

これは、$x$ の範囲が $a \le x \lt a+3$ なので、範囲の右側が頂点座標と一致する。

つまり、$a+3=1$ を解いて、$a=-2$ と分かります。

さらに、$a$ の値を大きくすると、$a=1$ で範囲の左側が頂点と一致します。

これらのことから、$-2 \lt a \lt 1$ において、最小値は頂点の $y$ 座標である１と分かります。

次に最大値について考えていきます。

最大値が変わるポイントは範囲の右側と左側の $y$ 座標が一致するときです。

二次関数は軸に対して対称なので、範囲の中心座標が軸と一致すれば良いことになります。

今回でいうと、$\displaystyle\frac{a+(a+3)}{2}=1$ より $a=-\displaystyle\frac{1}{2}$ と分かり、最大値 $f(a)$ になります。

STEP

最大値・最小値の変化のポイントを基にその他の範囲の最大値・最小値を求める。

では、その他の範囲も考えていきましょう。

STEP2で求めたポイント以外の範囲を考えます。

つまり、最小値においては $a \ge 1$ と $a \le -2$ ですが、グラフを見ればわかる通り、$a \ge 1$ のとき、最小値 $f(a)$、$a \le -2$ のとき、最小値なしとなります。

また、最大値においては $a \gt -\displaystyle\frac{1}{2}$ と $a \lt -\displaystyle\frac{1}{2}$ で、それぞれ、最大値なし、最大値 $f(a)$ となります。

STEP

求めた範囲を合わせて最終的な解答を出す。

$$\begin{align} &最大値 \begin{cases} なし & \left(a \gt -\displaystyle\frac{1}{2}\right) \\ f(a) & \left(a = -\displaystyle\frac{1}{2}\right) \\ f(a) & \left(a \lt -\displaystyle\frac{1}{2}\right) \end{cases} \\ &最小値 \begin{cases} f(a) & (a \ge 1) \\ 1 & (-2 \lt a \lt 1) \\ なし & (a \le -2) \end{cases} \end{align}$$

より、(最大値, 最小値)を $(f_{max}, f_{min})$ と表すことにして、範囲をまとめると

$$(f_{max}, f_{min}) = \begin{cases} (なし, a^2-2a+2) & (a \ge 1) \\ (なし, 1) & \left(-\frac{1}{2} \lt a \lt 1\right) \\ (a^2-2a+2, 1) & \left(-2 \lt a \le -\frac{1}{2}\right) \\ (a^2-2a+2, なし) & (a \lt -2) \end{cases}$$

補足

最大値・最小値の問題では、範囲が動く際に等号が成立するかの議論をする必要がある場合があります。

例えば、今回の場合は $a=1$ を $a \gt 1$ に含めても、$-\displaystyle\frac{1}{2} \lt a \lt 1$ に含めても問題ありません。

これは、$f(a)=a^2-2a+2$ において、$f(1)=1$ が成り立つからです。

このように、最大値・最小値は連続的に変化します。しかし、今回のように等号が含まれない範囲がある場合は等号成立がどちらの範囲に含まれるかを考える必要があります。

以下に例題を示します、解いてみてください。

例題

関数 $f(x)$ を下記のように定める。ただし、$a, b$ は整数

$$f(x)=-x^2-2ax-1　(b \le x \lt b+2)$$

このとき、下記の問いに答えよ

（１）$a=1$ のとき、$f(x)$ の最大値・最小値を求めよ。

（２）$b=1$ のとき、$f(x)$ の最大値・最小値を求めよ。

解答

（１）

$a=1$ のとき、$f(x)=-(x^2+2x+1)$ より $f(x)=-(x+1)^2　(b \le x \lt b+2)$

よって、グラフを図示すると以下のようになる。

（ⅰ）$b \le -3$ のとき

　　　最大値：なし、最小値：$f(b)=-b^2-2b-1$

（ⅱ）$-3 \lt b \le -2$ のとき

　　　最大値：０、最小値：$f(b)=-b^2-2b-1$

（ⅲ）$-2 \lt b \lt -1$ のとき

　　　最大値：０、最小値：なし

（ⅳ）$b \ge -1$ のとき

　　　最大値：$f(b)=-b^2-2b-1$、最小値：なし

（ⅰ）～（ⅳ）より、(最大値, 最小値)を $(f_{max}, f_{min})$ と表すことにして、範囲をまとめると

$$(f_{max}, f_{min}) = \begin{cases} (なし, -b^2-2b-1) & (b \le -3) \\ (0, -b^2-2b-1) &(-3 \lt b \le -2) \\ (0, なし) & (-2 \lt b \lt -1) \\ (-b^2-2b-1, なし) & (b \ge -1) \end{cases}$$

このように、記述する際は順番に場合分けを行い、それぞれ最大値・最小値を図を用いて説明するようにします。

しかし、最初からこのように考えるのは難しいので、前述したようなSTEPを得て答えを出した後に記述をするようにしてください。

（２）

$b=1$ のとき、$f(x)=-(x^2+2ax+1)$ より $f(x)=-(x+a)^2+a^2-1　(1 \le x \lt 3)$

グラフを図示すると以下のようになる。

（ⅰ）$a \le -3$ のとき

　　　最大値：なし、最小値：$f(1)=-2a-2$

（ⅱ）$-3 \lt a \le -2$ のとき

　　　最大値：$a^2-1$、最小値：$f(1)=-2a-2$

（ⅲ）$-2 \lt a \lt -1$ のとき

　　　最大値：$a^2-1$、最小値：なし

（ⅳ）$a \ge -1$ のとき

　　　最大値：$f(1)=-2a-2$、最小値：なし

（ⅰ）～（ⅳ）より、(最大値, 最小値)を $(f_{max}, f_{min})$ と表すことにして、範囲をまとめると

$$(f_{max}, f_{min}) = \begin{cases} (なし, -2a-2) & (a \le -3) \\ (a^2-1, -2a-2) &(-3 \lt a \le -2) \\ (a^2-2, なし) & (-2 \lt a \lt -1) \\ (-2a-2, なし) & (a \ge -1) \end{cases}$$

（２）は範囲が固定されていてグラフが移動するパターンです。場合分けのポイントは頂点が含まれるかと $y$ 座標が同じになるポイントがあるかなので前述のSTEP通りに進めれば同じように解けると思います。

うさぎさん

最大値・最小値の問題は数Ⅰ序盤の難関ポイントだよ

[応用]解を持つ条件・解の個数

ここからは、入試問題でも頻出の内容である、解を持つ条件と解の個数について扱っていきます。

解の個数は三次関数で聞かれる内容なのですが、今回は二次関数で考えていきます。

例

二次関数 $f(x)$ を下記のように定める。

$$f(x)=ax^2+bx+c$$

このとき、下記の問いに答えよ。

（１）$f(x)$ が実数解を持つ条件を求めよ。

（２）（１）で求めた条件式を $D$ としたとき、$D$ の値の場合分けによって解の個数を求めよ。

（３）$f(x)$ が正の実数解を持つ条件を求めよ。

（４）$f(x)$ が正と負の実数解を持つ条件を求めよ。

（５）$f(x)$ が $x \lt C, x \gt C$ の範囲に一つずつ実数解を持つ条件を求めよ。

（１）は判別式を答えればいいので

$$D=b^2-4ac$$

となります。実数解を持つ条件は重解も含めるので $D \ge 0$ です。

（２）は判別式の場合分けを答えれば良いので

$$解の個数 = \begin{cases} 2 & (D \gt 0) \\ 1 &(D = 0) \\ 0 & (D \lt 0) \end{cases}$$

となります。

（３）からが本題です。平方完成すると

$$f(x)=a \left( x+\displaystyle\frac{b}{2a}\right)^2-\displaystyle\frac{b^2}{4a}+c$$

となり、グラフを図示すると以下のようになります。

（３）から先はグラフを用いて考えていきます。実数解を持つ条件は（１）で求めたとおりです。

しかし、その条件しかない場合、負の実数解を持つ場合も考えられます。

そこで、注目すべきは $y$ 切片と軸の位置です。下に凸のグラフの場合で考えていきます。

まず、$y$ 切片は必ず正である必要があります。これは、グラフから明らかです。

また、そのとき、軸の位置が正であれば求める条件のなります。

二次関数が正の実数解を持つ条件

二次関数 $f(x)$ に対して

（ⅰ）判別式 $D \ge 0$

（ⅱ）下に凸の場合 $f(0) \gt 0$、上に凸の場合 $f(0) \lt 0$

（ⅲ）軸の値 $\gt 0$

注意すべきは下に凸か上に凸かで $y$ 切片の条件が変わる点ですが、グラフを図示すれば間違えることは無いと思います。

よって、解答としては $D=b^2-4ac$ として

$$(a \gt 0 の場合, a \lt 0 の場合) = \begin{cases} & (D \ge 0, D \ge 0) \\ & (c \gt 0, c \lt 0) \\ &(b \lt 0, b \gt 0) \end{cases}$$

$a$ の符号に応じて不等号が変化することだけ気を付けてください。

次に（４）ですが、これは条件が（３）に比べて簡単になります。

二次関数が正と負の実数解を持つ条件

二次関数 $f(x)$ に対して、下に凸の場合 $f(0) \lt 0$、上に凸の場合 $f(0) \gt 0$

実数解を持つ条件すら必要なくなりました。これは、この条件を満たしているとき、必ず実数解を持つからです。

これも、グラフから明らかです。確認してみてください。

よって、解答は $a \gt 0$ のとき、$c \lt 0$、$a \lt 0$ のとき、$c \gt 0$

最後に（５）ですが、これは、（４）の応用です。

（４）では、原点を基準にしてましたが（５）はある点 $C$ を基準にしているだけです。

二次関数がある点 $C$ において左右に実数解を持つ条件

二次関数 $f(x)$ に対して、下に凸の場合 $f(C) \lt 0$、上に凸の場合 $f(C) \gt 0$

よって、解答は $a \gt 0$ のとき、$aC^2+bC+c \lt 0$、$a \lt 0$ のとき、$aC^2+bC+c \gt 0$

うさぎさん

グラフをたくさん書いてみて、全てのグラフが条件を満たしてることを確認してみると良いよ

[応用]例題

二次関数 $f(x)$ と $g(x)$ を下記のように定める。

$$f(x)=ax^2$$

$$g(x)=x^2+bx+c$$

（１）$f(x), g(x)$ の共有点の個数を求めよ。[難]

（２）負の共有点を二つ持つ条件を求めよ。

（３）直線 $x=2$ から、$x$ 軸上での距離が等しい場所に共有点を持つ条件を求めよ。

解答

（１）

$h(x)=f(x)-g(x)$ とおくと、$h(x)=0$ を満たす実数解の個数と共有点の個数は一致する。

よって、$h(x)=(a-1)x^2-bx-c=0$ について考えていく。

（ⅰ）$h(x)$ が二次関数であるとき、つまり、$a \neq 1$ のとき、判別式 $D=b^2+4(a-1)c$ として

$$解の個数 = \begin{cases} 2 & (D \gt 0) \\ 1 &(D = 0) \\ 0 & (D \lt 0) \end{cases}$$

（ⅱ）$h(x)$ が一次関数であるとき、つまり、$a = 1$ かつ $b \neq 0$ のとき、解の個数は１

（ⅱ）$h(x)$ が直線であるとき、つまり、$a = 1$ かつ $b = 0$ のとき、

$$解の個数 = \begin{cases} \infty & (c = 0) \\ 0 &(c \neq 0) \end{cases}$$

（ⅰ）～（ⅲ）より、共有点の個数は $D = b^2+4(a-1)c$ として

$$共有点の個数 = \begin{cases} \infty & (a = 1 かつ b = 0 かつ c = 0) \\ 2 & (D \gt 0) \\ 1 &(D = 0, a = 1 かつ b \neq 0) \\ 0 & (D \lt 0, a = 1 かつ b = 0 かつ c \neq 0) \end{cases}$$

この問題は（１）が一番難しいと思います。

共有点とは$x, y$座標が一致すれば良いので $f(x)=g(x)$ を満たす実数解が存在すれば、それが共有点になり、実数解の個数が共有点の個数と一致します。

つまり、$h(x)=f(x)-g(x)$ とするとき、$h(x)=0$ を満たす実数解の個数を調べる問題に帰着します。

この考え方が難しいと思いますが、問題の数をこなすと分かるようになると思います。このような考え方があることは覚えておいてください。

さらに、この問いは $h(x)$ が$a, b$ の値に応じて二次関数や一次関数と変化するのも難しいポイントです。

判別式は二次関数のときにしか使えないので、そこで場合分けが必要になります。

以下に $f(x), g(x), h(x)$ のグラフを示すので値を変えて確認してみてください。

（２）

（１）の結果より、共有点が二つ存在するのは $h(x)$ が二次関数となるとき、よって、$a \neq 1$ とする。

$h(x)=0$ となる $x$ の値が共有点の座標より、$h(x)$ が $x \lt 0$ の範囲に二つの実数解を持つ条件を求める。グラフより次の三つの条件を満たせばよい、

（ⅰ）（１）の判別式を用いて $D \gt 0$

（ⅱ）$a \gt 1$ のとき、$c \lt 0$、$a \lt 1$ のとき、$c \gt 0$

（ⅲ）$a \gt 1$ のとき、$b \lt 0$、$a \lt 1$ のとき、$b \gt 0$

（ⅰ）～（ⅲ）より、求める条件は

$$(a \gt 0 の場合, a \lt 0 の場合) = \begin{cases} & (D \ge 0, D \ge 0) \\ & (c \lt 0, c \gt 0) \\ &(b \gt 0, b \lt 0) \end{cases}$$

（１）が分かればこの問題は前述の例とほとんど変わらないため簡単だと思います。平方完成するのが少し面倒ですが、基本的な手順に沿って解けば出来ますし、$f(x)=ax^2+bx+c$ を平方完成してから $a, b, c$ を $a-1, -b, -c$ に置き換えても解けます。

（３）

（１）の結果より、共有点が二つ存在するのは $h(x)$ が二次関数となるとき、よって、$a \neq 1$ とする。

$x=2$ からの $x$ 軸上での距離が等しい場所に共有点を持つということは、$h(x)$ の頂点が、直線 $x=2$ 上に存在し、下に凸の場合 $f(2) \lt 0$、上に凸の場合 $f(2) \gt 0$ を満たせばよい。

よって、求める条件は

$$(a \gt 0 の場合, a \lt 0 の場合) = \begin{cases} & (b = 4(a-1), b = 4(a-1)) \\ & (b \gt -c, b \lt -c) \end{cases}$$

これも、前述の例とほとんど同じですが一つ条件が追加されてます。

問題文を読んで知ってる問題と違う点を探し出し、それにあった条件を考える能力が記述問題では求められます。

これは、慣れが必要なので、多くの問題に触れてパターンを自分の中に蓄積してください。

最後に入試問題を解いてみてください

入試問題

二次関数 $\displaystyle y=\frac{3}{4}x^2-3x+4$ の区間 $a \le x \le b　(0 \lt a \lt b$\) における値域が区間 $a \le y \le b$ であるという。$a$ と $b$ の値を求めよ。

[1974 前期東工大]

解答

二次関数 $\displaystyle f(x)=y=\frac{3}{4}x^2-3x+4$ を平方完成すると $f(x)=\frac{3}{4}(x-2)^2+1$ となるから、図示すると

（ⅰ）$b \lt 2$ のとき

　　　最大値：$f(a)$、最小値：$f(b)$ となり、条件より

$$\begin{cases} \begin{eqnarray} & f(a)=\frac{3}{4}a^2-3a+4=b \tag{1} \\ & f(b)=\frac{3}{4}b^2-3b+4=a \tag{2} \end{eqnarray} \end{cases}$$

　　　（１）-（２）より

$$\begin{align} \frac{3}{4}(a^2-b^2)-3(a-b) & = b-a \\ (b-a)\left(\frac{3}{4}a+\frac{3}{4}b-2\right) & = 0 \end{align}$$

　　　$b \neq a$ より $\displaystyle b = \frac{8}{3} – a$ として（１）に代入すると

$$\begin{align} \frac{3}{4}a^2-3a+4 & = \frac{8}{3} – a\\ 9a^2-24a+16 & = 0 \\ (3a-4)^2 & = 0 \end{align}$$

　　　よって、$\displaystyle a=\frac{4}{3}, b=\frac{4}{3}$ となり、$b \neq a$ から不適。

（ⅱ）$0 \lt a \lt 2 \lt b$ かつ $a+b \lt 4$ のとき

　　　最大値：$f(a)$、最小値：１となり、条件より

$$\begin{cases} & a = 1 \\ & f(1)=\displaystyle\frac{3}{4} \cdot 1^2-3 \cdot 1 + 4 = b \end{cases}$$

　　　よって、$a, b) = (1, \displaystyle\frac{7}{4})$ となるが、$b \gt 2$ より不適。

（ⅲ）$0 \lt a \lt 2 \lt b$ かつ $a+b \ge 4$ のとき

　　　最大値：$f(b)$、最小値：１となり、条件より

$$\begin{cases} & a = 1 \\ & f(1)=\displaystyle\frac{3}{4}b^2-3b + 4 = b \end{cases}$$

$$\begin{align} \frac{3}{4}b^2-3b+4 & = b \\ 3b^2-16a+16 & = 0 \\ (3b-4)(b-4) & = 0 \end{align}$$

　　　となるから、$b=\displaystyle\frac{4}{3}, b=4$ となる、$b \gt 2$ より $b=4$

　　　よって、$(a, b) = (1, 4)$

（ⅳ）$a \gt 2$ のとき

　　　最大値：$f(a)$、最大値：$f(b)$ となり、条件より

$$\begin{cases} \begin{eqnarray} & f(a)=\frac{3}{4}a^2-3a+4=a \tag{1} \\ & f(b)=\frac{3}{4}b^2-3b+4=b \tag{2} \end{eqnarray} \end{cases}$$

　　　（１）（２）の解は共に $\displaystyle\frac{4}{3}, 4$ のいづれかになる。

　　　しかし、$a \gt 2, a \lt b$ を同時に満たす解の組は存在しないため不適

　　　（ⅰ）～（ⅳ）の結果より、求める $a, b$ の組は $(a, b)=(1, 4)$ のみ

よかったらシェアしてね！

URLをコピーしました！

URLをコピーしました！

基礎から学ぶ受験数学　＜関数編＞ ~二次関数~

二次関数

二次関数のグラフ

二次関数の最大値・最小値

[応用]解を持つ条件・解の個数

コメント

コメントするコメントをキャンセル

基礎から学ぶ受験数学 ＜関数編＞ ~二次関数~

二次関数

二次関数のグラフ

二次関数の最大値・最小値

[応用]解を持つ条件・解の個数

コメント

コメントする コメントをキャンセル

基礎から学ぶ受験数学　＜関数編＞ ~二次関数~

コメントするコメントをキャンセル